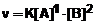A Cinética Química estuda a velocidade de uma reação química.
Velocidade Média de uma Reação (VM)
A velocidade média de uma reação em relação a um de seus componentes é a variação da quantidade desse componente ()q) na unidade de tempo.
A quantidade do componente por ser medida em moles ()q = )m), em concentração molar ()q = )M), etc.
É comum expressarmos a variação da quantidade em moles. Neste caso, teremos:
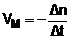 |
Para um reagente
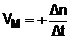 |
Para um produto
Onde:
VM à velocidade média da reação.
)n à variação do número de moles (números de moles final-número de moles inicial) num determinado intervalo de tempo.
)t à intervalo de tempo gasto.
Nota:
À medida que a reação vai se processando, os nos de moles de produtos vão aumentando; conseqüentemente o )n e VM serão positivos. Pelo contrário, o nº de moles de reagentes diminui com o tempo, o que nos proporcionaria )n e VM negativos. No intuito de evitar isto, trocamos o sinal algébrico do quociente )n/)t para os reagentes.
Ex.:
A cronometragem de reação X + Y à XY revelou os seguintes resultamos.
|
TEMPO (Minutos)
|
Nº DE MOLES PRESENTES DE X |
|
0 |
10 |
Calcular as velocidades médias dessa reação, em cada um dos intervalos mencionados.
a) De 2 a 8 minutos.
Solução:
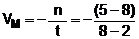
 |
b) De 5 a 10 minutos.
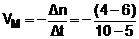
 |
Teoria das Colisões
Como vimos no capítulo anterior (Termoquímica), para haver uma reação, é necessário que haja colisão entre moléculas de reagentes, de modo que haja quebra de ligações para possibilitar a formação de novas ligações. Assim sendo, qualquer fator que venha a contribuir com um aumento na freqüência e/ou na intensidade destas colisões provocará um aumento na velocidade da reação. Desta forma, fica fácil compreendermos que um aumento da temperatura, da concentração dos reagentes ou da pressão (no caso de participantes gasosos) tende a provocar um aumento da velocidade da reação.
OBS.:
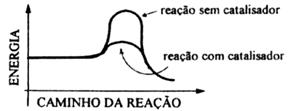
1) A velocidade de uma reação com os reagentes no estado gasoso é maior do que a velocidade da mesma reação com os reagentes no estado líquido e, esta por sua vez, maior do que a velocidade com os reagentes no estado sólido.
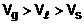 |
2) Quanto maior a superfície de contato entre os reagentes, maior a velocidade da reação. Desta forma, uma massa m de zinco em pó reage mais rapidamente com uma solução de ácido clorídrico do que uma placa de zinco de mesma massa m.
3) A introdução de um catalisador (substância que, quando misturada com os reagentes, possui a propriedade de diminuir a energia de ativação da reação) no sistema faz com que o complexo ativado e, conseqüentemente os produtos, sejam formados com maior facilidade. Desta forma, uma reação catalisada é mais rápida do que a mesma reação sem catalisador.
Lei da ação das massas (Guldberg-Waage)
“A velocidade de uma reação é diretamente proporcional às concentrações molares dos reagentes elevadas a expoentes que são iguais aos respectivos coeficientes da equação química ajustada”.
Deste modo, a equação de velocidade para uma reação do tipo a A (g) + b B (g) à c C (g) + d D (g) é:
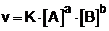 |
Onde:
v à velocidade da reação
k à constante de velocidade da reação (velocidade específica)
[A] à concentração molar do reagente A em moles por litro.
[B] à concentração molar do reagente B em moles por litro.
a à coeficientes do reagente A na equação ajustada.
b à coeficiente do reagente B na equação ajustada.
Ex.:
Dê a expressão de velocidade para as reações:
a) 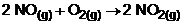
Aplicando da lei da ação das massas, teremos:
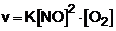 |
Nota:
A maioria das reações processam-se em várias etapas e, na maioria dos casos, as concentrações molares são elevadas a expoentes que não correspondem aos respectivos coeficientes da equação química ajustada. Nestes casos, os valores dos expoentes são determinados a partir de experiências.
Vejamos alguns exercícios resolvidos:
1) Seja a reação 2A + B à C + D. Suponhamos que a concentração de A seja triplicada e a de B seja duplicada. Que alteração sofre a velocidade da reação?
Solução:
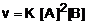
Chamaremos de x a concentração inicial de A e de y a concentração inicial de B.
Logo, inicialmente tmeos: 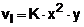
Depois fazemos: 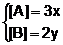
E passamos a ter:
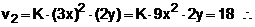
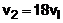 |
ou seja, a velocidade fica 18 vezes maior.
2) Calcule a velocidade, em moles/minuto, de produção de gás carbônico 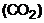 pela combustão completa de 4,448 litros segundo–1 de etano. Considere o volume medido nas CNTP.
pela combustão completa de 4,448 litros segundo–1 de etano. Considere o volume medido nas CNTP.
Solução:
velocidade de consumo de etano = 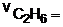
4,48 litros / segundo
velocidade de produção de gás carbônico =
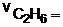 ? moles / minuto
? moles / minuto
Escrevendo a velocidade de consumo de etano na unidade pedida, teremos:
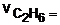 4,48 litros / segundo =
4,48 litros / segundo = 
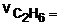 12 moles / minuto
12 moles / minuto
A equação de combustão do etano é:
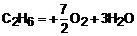
Pela equação acima vemos que para cada mol de 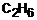 consumido, formam-se 2 moles de
consumido, formam-se 2 moles de 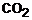 . Então, temos:
. Então, temos:
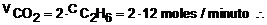
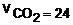 moles / minuto moles / minuto |
3) As substâncias A e B segundo a equação:
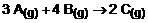
Essa reação não obedece à lei de Guldberg – Waage e sua equação de velocidade só pode ser determinada por exeriências. Estas nos oferecem os seguintes resultados:
|
Experiência |
[A] |
[B] |
Velocidade |
|
1 |
0,60 |
1,80 |
1,00 |
|
2 |
0,60 |
0,90 |
0,25 |
|
3 |
1,20 |
0,90 |
0,50 |
Sabendo que a equação de velocidade é 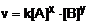 , calcule os valores de x e y.
, calcule os valores de x e y.
Solução:
Aplicando a equação de velocidade às três experiências, teremos:
Experiência 1: 1,00 = k . (0,6)x . (1,8)y ……(I)
Experiência 2: 0,25 = k . (0,6)x . (0,9)y ……(II)
Experiência 3: 0,50 = k . (1,2)x . (0,9)y ……(III)
Dividindo-se, membro a membro, a equação (I) pela equação (II), teremos:
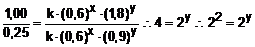
| y = 2 |
Dividindo-se membro a membro, a equação (III) pela equação (II), teremos:
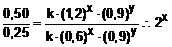
| x = 1 |
Observação:
A soma dos expoentes das concentrações na equação de velocidade é chamada de ordem da reação. Neste exercício, a ordem da reação (x + y) é igual a 3 (reações de 3ª ordem), uma vez que a equação de velocidade é